This class implements a feed-forward neural network. More...

#include <NeuralNetwork.h>

Collaboration diagram for nnp::NeuralNetwork:

[legend]

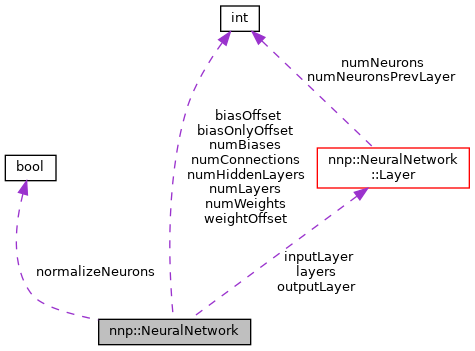
Classes
struct	Layer
	One neural network layer. More...

struct	Neuron
	A single neuron. More...

Public Types
enum	ActivationFunction { AF_UNSET , AF_IDENTITY , AF_TANH , AF_LOGISTIC , AF_SOFTPLUS , AF_RELU , AF_GAUSSIAN , AF_COS , AF_REVLOGISTIC , AF_EXP , AF_HARMONIC }
	List of available activation function types. More...

enum	ModificationScheme { MS_ZEROBIAS , MS_ZEROOUTPUTWEIGHTS , MS_FANIN , MS_GLOROTBENGIO , MS_NGUYENWIDROW , MS_PRECONDITIONOUTPUT }
	List of available connection modification schemes. More...

Public Member Functions
	NeuralNetwork (int numLayers, int const const &numNeuronsPerLayer, ActivationFunction const const &activationFunctionsPerLayer)
	Neural network class constructor. More...

	~NeuralNetwork ()

void	setNormalizeNeurons (bool normalizeNeurons)
	Turn on/off neuron normalization. More...

int	getNumNeurons () const
	Return total number of neurons. More...

int	getNumConnections () const
	Return total number of connections. More...

int	getNumWeights () const
	Return number of weights. More...

int	getNumBiases () const
	Return number of biases. More...

void	setConnections (double const *const &connections)
	Set neural network weights and biases. More...

void	getConnections (double *connections) const
	Get neural network weights and biases. More...

void	initializeConnectionsRandomUniform (unsigned int seed)
	Initialize connections with random numbers. More...

void	modifyConnections (ModificationScheme modificationScheme)
	Change connections according to a given modification scheme. More...

void	modifyConnections (ModificationScheme modificationScheme, double parameter1, double parameter2)
	Change connections according to a given modification scheme. More...

void	setInput (double const *const &input) const
	Set neural network input layer node values. More...

void	setInput (std::size_t const index, double const value) const
	Set neural network input layer node values. More...

void	getOutput (double *output) const
	Get neural network output layer node values. More...

void	propagate ()
	Propagate input information through all layers. More...

void	calculateDEdG (double *dEdG) const
	Calculate derivative of output neuron with respect to input neurons. More...

void	calculateDEdc (double *dEdc) const
	Calculate derivative of output neuron with respect to connections. More...

void	calculateDFdc (double dFdc, double const const &dGdxyz) const
	Calculate "second" derivative of output with respect to connections. More...

void	writeConnections (std::ofstream &file) const
	Write connections to file. More...

void	getNeuronStatistics (long count, double min, double max, double sum, double *sum2) const
	Return gathered neuron statistics. More...

void	resetNeuronStatistics ()
	Reset neuron statistics. More...

long	getMemoryUsage ()

std::vector< std::string >	info () const
	Print neural network architecture. More...

Private Member Functions
void	calculateDEdb (double *dEdb) const
	Calculate derivative of output neuron with respect to biases. More...

void	calculateDxdG (int index) const
	Calculate derivative of neuron values before activation function with respect to input neuron. More...

void	calculateD2EdGdc (int index, double const const &dEdb, double d2EdGdc) const
	Calculate second derivative of output neuron with respect to input neuron and connections. More...

void	allocateLayer (Layer &layer, int numNeuronsPrevLayer, int numNeurons, ActivationFunction activationFunction)
	Allocate a single layer. More...

void	propagateLayer (Layer &layer, Layer &layerPrev)
	Propagate information from one layer to the next. More...

Private Attributes
bool	normalizeNeurons
	If neurons are normalized. More...

int	numWeights
	Number of NN weights only. More...

int	numBiases
	Number of NN biases only. More...

int	numConnections
	Number of NN connections (weights + biases). More...

int	numLayers
	Total number of layers (includes input and output layers). More...

int	numHiddenLayers
	Number of hidden layers. More...

int *	weightOffset
	Offset adress of weights per layer in combined weights+bias array. More...

int *	biasOffset
	Offset adress of biases per layer in combined weights+bias array. More...

int *	biasOnlyOffset
	Offset adress of biases per layer in bias only array. More...

Layer *	inputLayer
	Pointer to input layer. More...

Layer *	outputLayer
	Pointer to output layer. More...

Layer *	layers
	Neural network layers. More...

Detailed Description

This class implements a feed-forward neural network.

Definition at line 28 of file NeuralNetwork.h.

Member Enumeration Documentation

◆ ActivationFunction

enum nnp::NeuralNetwork::ActivationFunction

List of available activation function types.

Enumerator
AF_UNSET	Unset activation function.
AF_IDENTITY	$f_a(x) = x$
AF_TANH	$f_a(x) = \tanh(x)$
AF_LOGISTIC	$f_a(x) = 1 / (1 + \mathrm{e}^{-x})$
AF_SOFTPLUS	$f_a(x) = \ln (1 + \mathrm{e}^x)$
AF_RELU	$f_a(x) = \max(0, x)$ (NOT recommended for HDNNPs!)
AF_GAUSSIAN	$f_a(x) = \mathrm{e}^{-x^2 / 2}$
AF_COS	$f_a(x) = \cos (x)$
AF_REVLOGISTIC	$f_a(x) = 1 - 1 / (1 + \mathrm{e}^{-x})$
AF_EXP	$f_a(x) = \mathrm{e}^{-x}$
AF_HARMONIC	$f_a(x) = x^2$

Definition at line 32 of file NeuralNetwork.h.

    {
        AF_UNSET,
        AF_IDENTITY,
        AF_TANH,
        AF_LOGISTIC,
        AF_SOFTPLUS,
        AF_RELU,
        AF_GAUSSIAN,
        AF_COS,
        AF_REVLOGISTIC,
        AF_EXP,
        AF_HARMONIC
    };

◆ ModificationScheme

enum nnp::NeuralNetwork::ModificationScheme

List of available connection modification schemes.

Enumerator
MS_ZEROBIAS	Set all bias values to zero.
MS_ZEROOUTPUTWEIGHTS	Set all weights connecting to the output layer to zero.
MS_FANIN	Normalize weights via number of neuron inputs (fan-in). If initial weights are uniformly distributed in @f$\left[-1, 1\right]@f$ they will be scaled to be in @f$\left[\frac{-1}{\sqrt{n_\text{in}}}, \frac{1}{\sqrt{n_\text{in}}}\right]@f$, where @f$n_\text{in}@f$ is the number of incoming weights of a neuron (if activation function is of type #AF_TANH).
MS_GLOROTBENGIO	Normalize connections according to Glorot and Bengio. If initial weights are uniformly distributed in @f$\left[-1, 1\right]@f$ they will be scaled to be in @f$\left[-\sqrt{\frac{6}{n_\text{in} + n_\text{out}}}, \sqrt{\frac{6}{n_\text{in} + n_\text{out}}}\right]@f$, where @f$n_\text{in}@f$ and @f$n_\text{out}@f$ are the number of incoming and outgoing weights of a neuron, respectively (if activation function is of type #AF_TANH). For details see: - X. Glorot and Y. Bengio, "Understanding the difficulty of training deep feedforward neural networks", International conference on artificial intelligence and statistics. 2010.
MS_NGUYENWIDROW	Initialize connections according to Nguyen-Widrow scheme. For details see: - D. Nguyen and B. Widrow, Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights, Proceedings of the International Joint Conference on Neural networks (IJCNN), pages 21-26, San Diego, 1990 - T. Morawietz, Entwicklung eines effizienten Potentials für das Wasser-Dimer basierend auf künstlichen neuronalen Netzen, Master's thesis, pages 24-28, Bochum, 2010
MS_PRECONDITIONOUTPUT	Apply preconditioning to output layer connections. Multiply weights connecting to output neurons with @f$\sigma@f$ and add "mean" to biases. Call #modifyConnections with two additional arguments: #modifyConnections(NeuralNetwork::MS_PRECONDITIONOUTPUT, mean, sigma);

Definition at line 59 of file NeuralNetwork.h.

    {
        MS_ZEROBIAS,
        MS_ZEROOUTPUTWEIGHTS,
        MS_FANIN,
        MS_GLOROTBENGIO,
        MS_NGUYENWIDROW,
        MS_PRECONDITIONOUTPUT
    };

Constructor & Destructor Documentation

◆ NeuralNetwork()

NeuralNetwork::NeuralNetwork	(	int	numLayers,
		int const *const &	numNeuronsPerLayer,
		ActivationFunction const *const &	activationFunctionsPerLayer
	)

Neural network class constructor.

Parameters

[in]	numLayers	Total number of layers (including in- and output layer).
[in]	numNeuronsPerLayer	Array with number of neurons per layer.
[in]	activationFunctionsPerLayer	Array with activation function type per layer (note: input layer activation function is is mandatory although it is never used).

Definition at line 30 of file NeuralNetwork.cpp.

{
    // check number of layers
    this->numLayers = numLayers;
    if (numLayers < 3)
    {
        fprintf(stderr,
                "ERROR: Neural network must have at least three layers\n");
        exit(EXIT_FAILURE);
    }
    numHiddenLayers = numLayers - 2;
 
    // do not normalize neurons by default
    normalizeNeurons = false;
 
    // allocate layers and populate with neurons
    layers = new Layer[numLayers];
    inputLayer = &layers[0];
    outputLayer = &layers[numLayers-1];
    allocateLayer(*inputLayer,
                  0,
                  numNeuronsPerLayer[0],
                  activationFunctionsPerLayer[0]);
    for (int i = 1; i < numLayers; i++)
    {
        allocateLayer(layers[i],
                      numNeuronsPerLayer[i-1],
                      numNeuronsPerLayer[i],
                      activationFunctionsPerLayer[i]);
    }
 
    // count connections
    numWeights     = 0;
    numBiases      = 0;
    numConnections = 0;
    for (int i = 1; i < numLayers; i++)
    {
        numBiases  += layers[i].numNeurons;
        numWeights += layers[i].numNeurons * layers[i].numNeuronsPrevLayer;
    }
    numConnections = numWeights + numBiases;
 
    // calculate weight and bias offsets for each layer
    weightOffset = new int[numLayers-1];
    weightOffset[0] = 0;
    for (int i = 1; i < numLayers-1; i++)
    {
        weightOffset[i] = weightOffset[i-1] +
                          (layers[i-1].numNeurons + 1) * layers[i].numNeurons;
    }
    biasOffset = new int[numLayers-1];
    for (int i = 0; i < numLayers-1; i++)
    {
        biasOffset[i] = weightOffset[i] +
                        layers[i+1].numNeurons * layers[i].numNeurons;
    }
    biasOnlyOffset = new int[numLayers-1];
    biasOnlyOffset[0] = 0;
    for (int i = 1; i < numLayers-1; i++)
    {
        biasOnlyOffset[i] = biasOnlyOffset[i-1] + layers[i].numNeurons;
    }
}

References allocateLayer(), biasOffset, biasOnlyOffset, inputLayer, layers, normalizeNeurons, numBiases, numConnections, numHiddenLayers, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, numWeights, outputLayer, and weightOffset.

Here is the call graph for this function:

◆ ~NeuralNetwork()

NeuralNetwork::~NeuralNetwork ( )

Definition at line 97 of file NeuralNetwork.cpp.

{
    for (int i = 0; i < numLayers; i++)
    {
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            delete[] layers[i].neurons[j].weights;
        }
        delete[] layers[i].neurons;
    }
    delete[] layers;
    delete[] weightOffset;
    delete[] biasOffset;
    delete[] biasOnlyOffset;
}

References biasOffset, biasOnlyOffset, layers, nnp::NeuralNetwork::Layer::neurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, weightOffset, and nnp::NeuralNetwork::Neuron::weights.

Member Function Documentation

◆ setNormalizeNeurons()

void NeuralNetwork::setNormalizeNeurons ( bool normalizeNeurons )

Turn on/off neuron normalization.

Parameters

[in] normalizeNeurons true or false (default: false).

Definition at line 113 of file NeuralNetwork.cpp.

{
    this->normalizeNeurons = normalizeNeurons;
 
    return;
}

References normalizeNeurons.

◆ getNumNeurons()

int NeuralNetwork::getNumNeurons ( ) const

Return total number of neurons.

Includes input and output layer.

Definition at line 120 of file NeuralNetwork.cpp.

{
    int count = 0;
 
    for (int i = 0; i < numLayers; i++)
    {
        count += layers[i].numNeurons;
    }
 
    return count;
}

References layers, numLayers, and nnp::NeuralNetwork::Layer::numNeurons.

Referenced by getMemoryUsage().

Here is the caller graph for this function:

◆ getNumConnections()

int NeuralNetwork::getNumConnections ( ) const

Return total number of connections.

Connections are all weights and biases.

Definition at line 132 of file NeuralNetwork.cpp.

{
    return numConnections;
}

References numConnections.

Referenced by nnp::Training::getWeights(), nnp::Training::randomizeNeuralNetworkWeights(), and nnp::Training::setWeights().

Here is the caller graph for this function:

◆ getNumWeights()

int NeuralNetwork::getNumWeights ( ) const

Return number of weights.

Definition at line 137 of file NeuralNetwork.cpp.

{
    return numWeights;
}

References numWeights.

◆ getNumBiases()

int NeuralNetwork::getNumBiases ( ) const

Return number of biases.

Definition at line 142 of file NeuralNetwork.cpp.

{
    return numBiases;
}

References numBiases.

◆ setConnections()

void NeuralNetwork::setConnections ( double const *const & connections )

Set neural network weights and biases.

Parameters

[in]

connections

One-dimensional array with neural network connections in the following order:

\[ \underbrace{ \overbrace{ a^{01}_{00}, \ldots, a^{01}_{0m_1}, a^{01}_{10}, \ldots, a^{01}_{1m_1}, \ldots, a^{01}_{n_00}, \ldots, a^{01}_{n_0m_1}, }^{\text{Weights}} \overbrace{ b^{1}_{0}, \ldots, b^{1}_{m_1} }^{\text{Biases}} }_{\text{Layer } 0 \rightarrow 1}, \underbrace{ a^{12}_{00}, \ldots, b^{2}_{m_2} }_{\text{Layer } 1 \rightarrow 2}, \ldots, \underbrace{ a^{p-1,p}_{00}, \ldots, b^{p}_{m_p} }_{\text{Layer } p-1 \rightarrow p} \]

where $a^{i-1, i}_{jk}$ is the weight connecting neuron $j$ in layer $i-1$ to neuron $k$ in layer $i$ and $b^{i}_{k}$ is the bias assigned to neuron $k$ in layer $i$.

Definition at line 147 of file NeuralNetwork.cpp.

{
    int count = 0;
 
    for (int i = 1; i < numLayers; i++)
    {
        for (int j = 0; j < layers[i].numNeuronsPrevLayer; j++)
        {
            for (int k = 0; k < layers[i].numNeurons; k++)
            {
                layers[i].neurons[k].weights[j] = connections[count];
                count++;
            }
        }
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            layers[i].neurons[j].bias = connections[count];
            count++;
        }
    }
 
    return;
}

References nnp::NeuralNetwork::Neuron::bias, layers, nnp::NeuralNetwork::Layer::neurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, and nnp::NeuralNetwork::Neuron::weights.

Referenced by initializeConnectionsRandomUniform(), nnp::Training::randomizeNeuralNetworkWeights(), nnp::Mode::readNeuralNetworkWeights(), and nnp::Training::setWeights().

Here is the caller graph for this function:

◆ getConnections()

void NeuralNetwork::getConnections ( double * connections ) const

Get neural network weights and biases.

Parameters

[out] connections One-dimensional array with neural network connections (same order as described in setConnections())

Definition at line 171 of file NeuralNetwork.cpp.

{
    int count = 0;
 
    for (int i = 1; i < numLayers; i++)
    {
        for (int j = 0; j < layers[i].numNeuronsPrevLayer; j++)
        {
            for (int k = 0; k < layers[i].numNeurons; k++)
            {
                connections[count] = layers[i].neurons[k].weights[j] ;
                count++;
            }
        }
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            connections[count] = layers[i].neurons[j].bias;
            count++;
        }
    }
 
    return;
}

References nnp::NeuralNetwork::Neuron::bias, layers, nnp::NeuralNetwork::Layer::neurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, and nnp::NeuralNetwork::Neuron::weights.

Referenced by nnp::Training::getWeights().

Here is the caller graph for this function:

◆ initializeConnectionsRandomUniform()

void NeuralNetwork::initializeConnectionsRandomUniform ( unsigned int seed )

Initialize connections with random numbers.

Parameters

[in] seed Random number generator seed.

Weights are initialized with random values in the $[-1, 1]$ interval. The C standard library rand() function is used.

Definition at line 195 of file NeuralNetwork.cpp.

{
    double* connections = new double[numConnections];
 
    srand(seed);
    for (int i = 0; i < numConnections; i++)
    {
        connections[i] = -1.0 + 2.0 * (double)rand() / RAND_MAX;
    }
 
    setConnections(connections);
 
    delete[] connections;
 
    return;
}

References numConnections, and setConnections().

Here is the call graph for this function:

◆ modifyConnections() [1/2]

void NeuralNetwork::modifyConnections ( ModificationScheme modificationScheme )

Change connections according to a given modification scheme.

Parameters

[in] modificationScheme Defines how the connections are modified. See ModificationScheme for possible options.

Definition at line 212 of file NeuralNetwork.cpp.

{
    if (modificationScheme == MS_ZEROBIAS)
    {
        for (int i = 0; i < numLayers; i++)
        {
            for (int j = 0; j < layers[i].numNeurons; j++)
            {
                layers[i].neurons[j].bias = 0.0;
            }
        }
    }
    else if (modificationScheme == MS_ZEROOUTPUTWEIGHTS)
    {
        for (int i = 0; i < outputLayer->numNeurons; i++)
        {
            for (int j = 0; j < outputLayer->numNeuronsPrevLayer; j++)
            {
                outputLayer->neurons[i].weights[j] = 0.0;
            }
        }
    }
    else if (modificationScheme == MS_FANIN)
    {
        for (int i = 1; i < numLayers; i++)
        {
            if(layers[i].activationFunction == AF_TANH)
            {
                for (int j = 0; j < layers[i].numNeurons; j++)
                {
                    for (int k = 0; k < layers[i].numNeuronsPrevLayer; k++)
                    {
                        layers[i].neurons[j].weights[k] /=
                                           sqrt(layers[i].numNeuronsPrevLayer);
                    }
                }
            }
        }
    }
    else if (modificationScheme == MS_GLOROTBENGIO)
    {
        for (int i = 1; i < numLayers; i++)
        {
            if(layers[i].activationFunction == AF_TANH)
            {
                for (int j = 0; j < layers[i].numNeurons; j++)
                {
                    for (int k = 0; k < layers[i].numNeuronsPrevLayer; k++)
                    {
                        layers[i].neurons[j].weights[k] *= sqrt(6.0 / (
                                             layers[i].numNeuronsPrevLayer
                                           + layers[i].numNeurons));
                    }
                }
            }
        }
    }
    else if (modificationScheme == MS_NGUYENWIDROW)
    {
        double beta   = 0.0;
        double sum    = 0.0;
        double weight = 0.0;
 
        for (int i = 1; i < numLayers-1; i++)
        {
            beta = 0.7 * pow(layers[i].numNeurons,
                             1.0 / double(layers[i].numNeuronsPrevLayer));
            for (int j = 0; j < layers[i].numNeurons; j++)
            {
                sum = 0.0;
                for (int k = 0; k < layers[i].numNeuronsPrevLayer; k++)
                {
                    weight = layers[i].neurons[j].weights[k];
                    sum += weight * weight;
                }
                sum = sqrt(sum);
                for (int k = 0; k < layers[i].numNeuronsPrevLayer; k++)
                {
                    layers[i].neurons[j].weights[k] *= beta / sum;
                    if (layers[i].activationFunction == AF_TANH)
                    {
                        layers[i].neurons[j].weights[k] *= 2.0;
                    }
                }
                layers[i].neurons[j].bias *= beta;
                if (layers[i].activationFunction == AF_TANH)
                {
                    layers[i].neurons[j].bias *= 2.0;
                }
            }
        }
        for (int i = 0; i < outputLayer->numNeurons; i++)
        {
            outputLayer->neurons[0].weights[i] *= 0.5;
        }
    }
    else
    {
        fprintf(stderr, "ERROR: Incorrect modifyConnections call.\n");
        exit(EXIT_FAILURE);
    }
 
    return;
}

References AF_TANH, nnp::NeuralNetwork::Neuron::bias, layers, MS_FANIN, MS_GLOROTBENGIO, MS_NGUYENWIDROW, MS_ZEROBIAS, MS_ZEROOUTPUTWEIGHTS, nnp::NeuralNetwork::Layer::neurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, outputLayer, and nnp::NeuralNetwork::Neuron::weights.

Referenced by nnp::Training::randomizeNeuralNetworkWeights().

Here is the caller graph for this function:

◆ modifyConnections() [2/2]

void NeuralNetwork::modifyConnections	(	ModificationScheme	modificationScheme,
		double	parameter1,
		double	parameter2
	)

Change connections according to a given modification scheme.

Parameters

[in]	modificationScheme	Defines how the connections are modified. See ModificationScheme for possible options.
[in]	parameter1	Additional parameter (see ModificationScheme).
[in]	parameter2	Additional parameter (see ModificationScheme).

Definition at line 317 of file NeuralNetwork.cpp.

{
    if (modificationScheme == MS_PRECONDITIONOUTPUT)
    {
        double mean  = parameter1;
        double sigma = parameter2;
 
        for (int i = 0; i < outputLayer->numNeurons; i++)
        {
            for (int j = 0; j < outputLayer->numNeuronsPrevLayer; j++)
            {
                outputLayer->neurons[i].weights[j] *= sigma;
            }
            outputLayer->neurons[i].bias += mean;
        }
    }
    else
    {
        fprintf(stderr, "ERROR: Incorrect modifyConnections call.\n");
        exit(EXIT_FAILURE);
    }
 
    return;
}

References nnp::NeuralNetwork::Neuron::bias, MS_PRECONDITIONOUTPUT, nnp::NeuralNetwork::Layer::neurons, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, outputLayer, and nnp::NeuralNetwork::Neuron::weights.

◆ setInput() [1/2]

void NeuralNetwork::setInput ( double const *const & input ) const

Set neural network input layer node values.

Parameters

[in] input Input layer node values.

Definition at line 357 of file NeuralNetwork.cpp.

{
    for (int i = 0; i < inputLayer->numNeurons; i++)
    {
        // TODO: replace by calling setInput from above
        // also, for 4G we need charges
        double const& value = input[i];
        Neuron& n = inputLayer->neurons[i];
        n.count++;
        n.value = value;
        n.min  = min(value, n.min);
        n.max  = max(value, n.max);
        n.sum  += value;
        n.sum2 += value * value;
    }
 
    return;
}

References nnp::NeuralNetwork::Neuron::count, inputLayer, nnp::NeuralNetwork::Neuron::max, nnp::NeuralNetwork::Neuron::min, nnp::NeuralNetwork::Layer::neurons, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Neuron::sum, nnp::NeuralNetwork::Neuron::sum2, and nnp::NeuralNetwork::Neuron::value.

Referenced by nnp::Mode::calculateAtomicNeuralNetworks(), nnp::Training::calculateWeightDerivatives(), nnp::Training::dPdc(), and nnp::Training::update().

Here is the caller graph for this function:

◆ setInput() [2/2]

void nnp::NeuralNetwork::setInput	(	std::size_t const	index,
		double const	value
	)		const

Set neural network input layer node values.

Parameters

[in]	index	Index of neuron to set.
[in]	value	Input layer neuron value.

◆ getOutput()

void NeuralNetwork::getOutput ( double * output ) const

Get neural network output layer node values.

Parameters

[out] output Output layer node values.

Definition at line 376 of file NeuralNetwork.cpp.

{
    for (int i = 0; i < outputLayer->numNeurons; i++)
    {
        output[i] = outputLayer->neurons[i].value;
    }
 
    return;
}

References nnp::NeuralNetwork::Layer::neurons, nnp::NeuralNetwork::Layer::numNeurons, outputLayer, and nnp::NeuralNetwork::Neuron::value.

Referenced by nnp::Mode::calculateAtomicNeuralNetworks(), nnp::Training::calculateWeightDerivatives(), nnp::Training::dPdc(), and nnp::Training::update().

Here is the caller graph for this function:

◆ propagate()

void NeuralNetwork::propagate ( )

Propagate input information through all layers.

With the input data set by setInput() this will calculate all remaining neuron values, the output in the last layer is acccessible via getOutput().

Definition at line 386 of file NeuralNetwork.cpp.

{
    for (int i = 1; i < numLayers; i++)
    {
        propagateLayer(layers[i], layers[i-1]);
    }
 
    return;
}

References layers, numLayers, and propagateLayer().

Referenced by nnp::Mode::calculateAtomicNeuralNetworks(), nnp::Training::calculateWeightDerivatives(), nnp::Training::dPdc(), and nnp::Training::update().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ calculateDEdG()

void NeuralNetwork::calculateDEdG ( double * dEdG ) const

Calculate derivative of output neuron with respect to input neurons.

Parameters

[out] dEdG Array containing derivative (length is number of input neurons).

CAUTION: This works only for neural networks with a single output neuron!

Returns $\left(\frac{dE}{dG_i}\right)_{i=1,\ldots,N}$, where $E$ is the output neuron and $\left(G_i\right)_{i=1,\ldots,N}$ are the $N$ input neurons.

Definition at line 396 of file NeuralNetwork.cpp.

{
    double** inner = new double*[numHiddenLayers];
    double** outer = new double*[numHiddenLayers];
 
    for (int i = 0; i < numHiddenLayers; i++)
    {
        inner[i] = new double[layers[i+1].numNeurons];
        outer[i] = new double[layers[i+2].numNeurons];
    }
 
    for (int k = 0; k < layers[0].numNeurons; k++)
    {
        for (int i = 0; i < layers[1].numNeurons; i++)
        {
            inner[0][i] = layers[1].neurons[i].weights[k]
                        * layers[1].neurons[i].dfdx;
            if (normalizeNeurons) inner[0][i] /= layers[0].numNeurons;
        }
        for (int l = 1; l < numHiddenLayers+1; l++)
        {
            for (int i2 = 0; i2 < layers[l+1].numNeurons; i2++)
            {
                outer[l-1][i2] = 0.0;
                for (int i1 = 0; i1 < layers[l].numNeurons; i1++)
                {
                    outer[l-1][i2] += layers[l+1].neurons[i2].weights[i1]
                                    * inner[l-1][i1];
                }
                outer[l-1][i2] *= layers[l+1].neurons[i2].dfdx;
                if (normalizeNeurons) outer[l-1][i2] /= layers[l].numNeurons;
                if (l < numHiddenLayers) inner[l][i2] = outer[l-1][i2];
            }
        }
        dEdG[k] = outer[numHiddenLayers-1][0];
    }
 
    for (int i = 0; i < numHiddenLayers; i++)
    {
        delete[] inner[i];
        delete[] outer[i];
    }
    delete[] inner;
    delete[] outer;
 
    return;
}

References nnp::NeuralNetwork::Neuron::dfdx, layers, nnp::NeuralNetwork::Layer::neurons, normalizeNeurons, numHiddenLayers, nnp::NeuralNetwork::Layer::numNeurons, and nnp::NeuralNetwork::Neuron::weights.

Referenced by nnp::Mode::calculateAtomicNeuralNetworks(), nnp::Training::dPdc(), and nnp::Training::update().

Here is the caller graph for this function:

◆ calculateDEdc()

void NeuralNetwork::calculateDEdc ( double * dEdc ) const

Calculate derivative of output neuron with respect to connections.

Parameters

[out] dEdc Array containing derivative (length is number of connections, see getNumConnections()).

CAUTION: This works only for neural networks with a single output neuron!

Returns $\left(\frac{dE}{dc_i}\right)_{i=1,\ldots,N}$, where $E$ is the output neuron and $\left(c_i\right)_{i=1,\ldots,N}$ are the $N$ connections (weights and biases) of the neural network. See setConnections() for details on the order of weights an biases.

Definition at line 444 of file NeuralNetwork.cpp.

{
    int count = 0;
 
    for (int i = 0; i < numConnections; i++)
    {
        dEdc[i] = 0.0;
    }
 
    for (int i = 0; i < outputLayer->numNeurons; i++)
    {
        dEdc[biasOffset[numLayers-2]+i] = outputLayer->neurons[i].dfdx;
        if (normalizeNeurons)
        {
            dEdc[biasOffset[numLayers-2]+i] /=
                outputLayer->numNeuronsPrevLayer;
        }
    }
 
    for (int i = numLayers-2; i >= 0; i--)
    {
        count = 0;
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            for (int k = 0; k < layers[i+1].numNeurons; k++)
            {
                dEdc[weightOffset[i]+count] = dEdc[biasOffset[i]+k]
                                            * layers[i].neurons[j].value;
                count++;
                if (i >= 1)
                {
                    dEdc[biasOffset[i-1]+j] += dEdc[biasOffset[i]+k]
                        * layers[i+1].neurons[k].weights[j]
                        * layers[i].neurons[j].dfdx;
                }
            }
            if (normalizeNeurons && i >= 1)
            {
                dEdc[biasOffset[i-1]+j] /= layers[i].numNeuronsPrevLayer;
            }
        }
    }
 
    return;
}

References biasOffset, nnp::NeuralNetwork::Neuron::dfdx, layers, nnp::NeuralNetwork::Layer::neurons, normalizeNeurons, numConnections, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, outputLayer, nnp::NeuralNetwork::Neuron::value, weightOffset, and nnp::NeuralNetwork::Neuron::weights.

Referenced by nnp::Training::calculateWeightDerivatives(), nnp::Training::dPdc(), and nnp::Training::update().

Here is the caller graph for this function:

◆ calculateDFdc()

void NeuralNetwork::calculateDFdc	(	double *	dFdc,
		double const *const &	dGdxyz
	)		const

Calculate "second" derivative of output with respect to connections.

Parameters

[out]	dFdc	Array containing derivative (length is number of connections, see getNumConnections()).
[in]	dGdxyz	Array containing derivative of input neurons with respect to coordinates $\frac{\partial G_j} {\partial x_{l, \gamma}}$.

CAUTION: This works only for neural networks with a single output neuron!

In the context of the neural network potentials this function is used to calculate derivatives of forces (or force contributions) with respect to connections. The force component $\gamma$ (where $\gamma$ is one of $x,y,z$) of particle $l$ is

\[ F_{l, \gamma} = - \frac{\partial}{\partial x_{l, \gamma}} \sum_i^{N} E_i = - \sum_i^N \sum_j^M \frac{\partial E_i}{\partial G_j} \frac{\partial G_j}{\partial x_{l, \gamma}}, \]

where $N$ is the number of particles in the system and $M$ is the number of symmetry functions (number of input neurons). Hence the derivative of $F_{l, \gamma}$ with respect to the neural network connection $c_n$ is

\[ \frac{\partial}{\partial c_n} F_{l, \gamma} = - \sum_i^N \sum_j^M \frac{\partial^2 E_i}{\partial c_n \partial G_j} \frac{\partial G_j}{\partial x_{l, \gamma}}. \]

Thus, with given $\frac{\partial G_j}{\partial x_{l, \gamma}}$ this function calculates

\[ \sum_j^M \frac{\partial^2 E}{\partial c_n \partial G_j} \frac{\partial G_j}{\partial x_{l, \gamma}} \]

for the current network status and returns it via the output array.

Definition at line 490 of file NeuralNetwork.cpp.

{
    double* dEdb    = new double[numBiases];
    double* d2EdGdc = new double[numConnections];
 
    for (int i = 0; i < numBiases; i++)
    {
        dEdb[i] = 0.0;
    }
    for (int i = 0; i < numConnections; i++)
    {
        dFdc[i]    = 0.0;
        d2EdGdc[i] = 0.0;
    }
 
    calculateDEdb(dEdb);
    for (int i = 0; i < layers[0].numNeurons; i++)
    {
        for (int j = 0; j < numConnections; j++)
        {
            d2EdGdc[j] = 0.0;
        }
        calculateDxdG(i);
        calculateD2EdGdc(i, dEdb, d2EdGdc);
        for (int j = 0; j < numConnections; j++)
        {
            // Note: F = - dE / dx !!
            //           ^
            dFdc[j] -= d2EdGdc[j] * dGdxyz[i];
        }
    }
 
    delete[] dEdb;
    delete[] d2EdGdc;
 
    return;
}

References calculateD2EdGdc(), calculateDEdb(), calculateDxdG(), layers, numBiases, numConnections, and nnp::NeuralNetwork::Layer::numNeurons.

Referenced by nnp::Training::calculateWeightDerivatives(), nnp::Training::dPdc(), and nnp::Training::update().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ writeConnections()

void NeuralNetwork::writeConnections ( std::ofstream & file ) const

Write connections to file.

Parameters

[in,out] file File stream to write to.

Definition at line 529 of file NeuralNetwork.cpp.

{
    // File header.
    vector<string> title;
    vector<string> colName;
    vector<string> colInfo;
    vector<size_t> colSize;
    title.push_back("Neural network connection values (weights and biases).");
    colSize.push_back(24);
    colName.push_back("connection");
    colInfo.push_back("Neural network connection value.");
    colSize.push_back(1);
    colName.push_back("t");
    colInfo.push_back("Connection type (a = weight, b = bias).");
    colSize.push_back(9);
    colName.push_back("index");
    colInfo.push_back("Index enumerating weights.");
    colSize.push_back(5);
    colName.push_back("l_s");
    colInfo.push_back("Starting point layer (end point layer for biases).");
    colSize.push_back(5);
    colName.push_back("n_s");
    colInfo.push_back("Starting point neuron in starting layer (end point "
                      "neuron for biases).");
    colSize.push_back(5);
    colName.push_back("l_e");
    colInfo.push_back("End point layer.");
    colSize.push_back(5);
    colName.push_back("n_e");
    colInfo.push_back("End point neuron in end layer.");
    appendLinesToFile(file,
                      createFileHeader(title, colSize, colName, colInfo));
 
    int count = 0;
    for (int i = 1; i < numLayers; i++)
    {
        for (int j = 0; j < layers[i].numNeuronsPrevLayer; j++)
        {
            for (int k = 0; k < layers[i].numNeurons; k++)
            {
                count++;
                file << strpr("%24.16E a %9d %5d %5d %5d %5d\n",
                              layers[i].neurons[k].weights[j],
                              count,
                              i - 1,
                              j + 1,
                              i,
                              k + 1);
            }
        }
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            count++;
            file << strpr("%24.16E b %9d %5d %5d\n",
                          layers[i].neurons[j].bias,
                          count,
                          i,
                          j + 1);
        }
    }
 
    return;
}

References nnp::appendLinesToFile(), nnp::createFileHeader(), layers, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, and nnp::strpr().

Here is the call graph for this function:

◆ getNeuronStatistics()

void NeuralNetwork::getNeuronStatistics	(	long *	count,
		double *	min,
		double *	max,
		double *	sum,
		double *	sum2
	)		const

Return gathered neuron statistics.

Parameters

[out]	count	Number of neuron output value calculations.
[out]	min	Minimum neuron value encountered.
[out]	max	Maximum neuron value encountered.
[out]	sum	Sum of all neuron values encountered.
[out]	sum2	Sum of squares of all neuron values encountered.

CAUTION: This works only for neural networks with a single output neuron!

When neuron values are calculated (e.g. when propagate() is called) statistics about encountered values are automatically gathered. The internal counters can be reset calling resetNeuronStatistics(). Neuron values are ordered layer by layer:

\[ \underbrace{y^0_1, \ldots, y^0_{N_0}}_\text{Input layer}, \underbrace{y^1_1, \ldots, y^1_{N_1}}_{\text{Hidden Layer } 1}, \ldots, \underbrace{y^p_1, \ldots, y^p_{N_p}}_\text{Output layer}, \]

where $y^m_i$ is neuron $i$ in layer $m$ and $N_m$ is the total number of neurons in this layer.

Definition at line 915 of file NeuralNetwork.cpp.

{
    int iNeuron = 0;
 
    for (int i = 0; i < numLayers; i++)
    {
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            count[iNeuron] = layers[i].neurons[j].count;
            min  [iNeuron] = layers[i].neurons[j].min;
            max  [iNeuron] = layers[i].neurons[j].max;
            sum  [iNeuron] = layers[i].neurons[j].sum;
            sum2 [iNeuron] = layers[i].neurons[j].sum2;
            iNeuron++;
        }
    }
 
    return;
}

References nnp::NeuralNetwork::Neuron::count, layers, nnp::NeuralNetwork::Neuron::max, nnp::NeuralNetwork::Neuron::min, nnp::NeuralNetwork::Layer::neurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Neuron::sum, and nnp::NeuralNetwork::Neuron::sum2.

◆ resetNeuronStatistics()

void NeuralNetwork::resetNeuronStatistics ( )

Reset neuron statistics.

Counters and summation variables for neuron statistics are reset.

Definition at line 898 of file NeuralNetwork.cpp.

{
    for (int i = 0; i < numLayers; i++)
    {
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            layers[i].neurons[j].count = 0;
            layers[i].neurons[j].min   =  numeric_limits<double>::max();
            layers[i].neurons[j].max   = -numeric_limits<double>::max();
            layers[i].neurons[j].sum   = 0.0;
            layers[i].neurons[j].sum2  = 0.0;
        }
    }
 
    return;
}

References nnp::NeuralNetwork::Neuron::count, layers, nnp::NeuralNetwork::Neuron::max, nnp::NeuralNetwork::Neuron::min, nnp::NeuralNetwork::Layer::neurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Neuron::sum, and nnp::NeuralNetwork::Neuron::sum2.

◆ getMemoryUsage()

long NeuralNetwork::getMemoryUsage ( )

Definition at line 981 of file NeuralNetwork.cpp.

{
    long mem        = sizeof(*this);
    int  numNeurons = getNumNeurons();
 
    mem += (numLayers - 1) * sizeof(int); // weightOffset
    mem += (numLayers - 1) * sizeof(int); // biasOffset
    mem += (numLayers - 1) * sizeof(int); // biasOnlyOffset
    mem += numLayers  * sizeof(Layer);    // layers
    mem += numNeurons * sizeof(Neuron);   // neurons
    mem += numWeights * sizeof(double);   // weights
 
    return mem;
}

References getNumNeurons(), numLayers, and numWeights.

Here is the call graph for this function:

◆ info()

vector< string > NeuralNetwork::info ( ) const

Print neural network architecture.

Definition at line 996 of file NeuralNetwork.cpp.

{
    vector<string> v;
    int maxNeurons = 0;
 
    v.push_back(strpr("Number of weights    : %6zu\n", numWeights));
    v.push_back(strpr("Number of biases     : %6zu\n", numBiases));
    v.push_back(strpr("Number of connections: %6zu\n", numConnections));
    v.push_back(strpr("Architecture    "));
    for (int i = 0; i < numLayers; ++i)
    {
        maxNeurons = max(layers[i].numNeurons, maxNeurons);
        v.push_back(strpr(" %4d", layers[i].numNeurons));
    }
    v.push_back("\n");
    v.push_back("-----------------------------------------"
                "--------------------------------------\n");
 
    for (int i = 0; i < maxNeurons; ++i)
    {
        v.push_back(strpr("%4d", i + 1));
        string s = "";
        for (int j = 0; j < numLayers; ++j)
        {
            if (i < layers[j].numNeurons)
            {
                if (j == 0)
                {
                    s += strpr(" %3s", "G");
                }
                else if (layers[j].activationFunction == AF_IDENTITY)
                {
                    s += strpr(" %3s", "l");
                }
                else if (layers[j].activationFunction == AF_TANH)
                {
                    s += strpr(" %3s", "t");
                }
                else if (layers[j].activationFunction == AF_LOGISTIC)
                {
                    s += strpr(" %3s", "s");
                }
                else if (layers[j].activationFunction == AF_SOFTPLUS)
                {
                    s += strpr(" %3s", "p");
                }
                else if (layers[j].activationFunction == AF_RELU)
                {
                    s += strpr(" %3s", "r");
                }
                else if (layers[j].activationFunction == AF_GAUSSIAN)
                {
                    s += strpr(" %3s", "g");
                }
                else if (layers[j].activationFunction == AF_COS)
                {
                    s += strpr(" %3s", "c");
                }
                else if (layers[j].activationFunction == AF_REVLOGISTIC)
                {
                    s += strpr(" %3s", "S");
                }
                else if (layers[j].activationFunction == AF_EXP)
                {
                    s += strpr(" %3s", "e");
                }
                else if (layers[j].activationFunction == AF_HARMONIC)
                {
                    s += strpr(" %3s", "h");
                }
            }
            else
            {
                s += "    ";
            }
        }
        v.push_back(s += "\n");
    }
 
    return v;
}

References AF_COS, AF_EXP, AF_GAUSSIAN, AF_HARMONIC, AF_IDENTITY, AF_LOGISTIC, AF_RELU, AF_REVLOGISTIC, AF_SOFTPLUS, AF_TANH, layers, numBiases, numConnections, numLayers, numWeights, and nnp::strpr().

Here is the call graph for this function:

◆ calculateDEdb()

void NeuralNetwork::calculateDEdb ( double * dEdb ) const

private

Calculate derivative of output neuron with respect to biases.

Parameters

[out] dEdb Array containing derivatives (length is number of biases).

CAUTION: This works only for neural networks with a single output neuron!

Similar to calculateDEdc() but includes only biases. Used internally by calculateDFdc().

Definition at line 593 of file NeuralNetwork.cpp.

{
    for (int i = 0; i < outputLayer->numNeurons; i++)
    {
        dEdb[biasOnlyOffset[numLayers-2]+i] = outputLayer->neurons[i].dfdx;
        if (normalizeNeurons)
        {
            dEdb[biasOnlyOffset[numLayers-2]+i] /=
                outputLayer->numNeuronsPrevLayer;
        }
    }
 
    for (int i = numLayers-2; i >= 0; i--)
    {
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            for (int k = 0; k < layers[i+1].numNeurons; k++)
            {
                if (i >= 1)
                {
                    dEdb[biasOnlyOffset[i-1]+j] += dEdb[biasOnlyOffset[i]+k]
                        * layers[i+1].neurons[k].weights[j]
                        * layers[i].neurons[j].dfdx;
                }
            }
            if (normalizeNeurons && i >= 1)
            {
                dEdb[biasOnlyOffset[i-1]+j] /= layers[i].numNeuronsPrevLayer;
            }
        }
    }
 
    return;
}

References biasOnlyOffset, nnp::NeuralNetwork::Neuron::dfdx, layers, nnp::NeuralNetwork::Layer::neurons, normalizeNeurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, outputLayer, and nnp::NeuralNetwork::Neuron::weights.

Referenced by calculateDFdc().

Here is the caller graph for this function:

◆ calculateDxdG()

void NeuralNetwork::calculateDxdG ( int index ) const

private

Calculate derivative of neuron values before activation function with respect to input neuron.

Parameters

[in] index Index of input neuron the derivative will be calculated for.

No output, derivatives are internally saved for each neuron in Neuron::dxdG. Used internally by calculateDFdc().

Definition at line 628 of file NeuralNetwork.cpp.

{
    for (int i = 0; i < layers[1].numNeurons; i++)
    {
        layers[1].neurons[i].dxdG = layers[1].neurons[i].weights[index];
        if (normalizeNeurons)
        {
            layers[1].neurons[i].dxdG /= layers[1].numNeuronsPrevLayer;
        }
    }
    for (int i = 2; i < numLayers; i++)
    {
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            layers[i].neurons[j].dxdG = 0.0;
            for (int k = 0; k < layers[i-1].numNeurons; k++)
            {
                layers[i].neurons[j].dxdG += layers[i].neurons[j].weights[k]
                                           * layers[i-1].neurons[k].dfdx
                                           * layers[i-1].neurons[k].dxdG;
            }
            if (normalizeNeurons)
            {
                layers[i].neurons[j].dxdG /= layers[i].numNeuronsPrevLayer;
            }
        }
    }
 
    return;
}

References nnp::NeuralNetwork::Neuron::dfdx, nnp::NeuralNetwork::Neuron::dxdG, layers, nnp::NeuralNetwork::Layer::neurons, normalizeNeurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, and nnp::NeuralNetwork::Neuron::weights.

Referenced by calculateDFdc().

Here is the caller graph for this function:

◆ calculateD2EdGdc()

void NeuralNetwork::calculateD2EdGdc	(	int	index,
		double const *const &	dEdb,
		double *	d2EdGdc
	)		const

private

Calculate second derivative of output neuron with respect to input neuron and connections.

Parameters

[in]	index	Index of input neuron the derivative will be calculated for.
[in]	dEdb	Derivatives of output neuron with respect to biases. See calculateDEdb().
[out]	d2EdGdc	Array containing the derivatives (ordered as described in setConnections()).

CAUTION: This works only for neural networks with a single output neuron!

Used internally by calculateDFdc().

Definition at line 659 of file NeuralNetwork.cpp.

{
    int count = 0;
 
    for (int i = 0; i < outputLayer->numNeurons; i++)
    {
        d2EdGdc[biasOffset[numLayers-2]+i] = outputLayer->neurons[i].d2fdx2
                                           * outputLayer->neurons[i].dxdG;
        if (normalizeNeurons)
        {
            d2EdGdc[biasOffset[numLayers-2]+i] /=
                outputLayer->numNeuronsPrevLayer;
        }
    }
 
    for (int i = numLayers-2; i >= 0; i--)
    {
        count = 0;
        for (int j = 0; j < layers[i].numNeurons; j++)
        {
            for (int k = 0; k < layers[i+1].numNeurons; k++)
            {
                if (i == 0)
                {
                    d2EdGdc[weightOffset[i]+count] =
                        d2EdGdc[biasOffset[i]+k] * layers[i].neurons[j].value;
                    if (j == index)
                    {
                        d2EdGdc[weightOffset[i]+count] +=
                            dEdb[biasOnlyOffset[i]+k];
                    }
                }
                else
                {
                    d2EdGdc[weightOffset[i]+count] =
                        d2EdGdc[biasOffset[i]+k] * layers[i].neurons[j].value
                      + dEdb[biasOnlyOffset[i]+k] * layers[i].neurons[j].dfdx
                      * layers[i].neurons[j].dxdG;
                }
                count++;
                if (i >= 1)
                {
                    d2EdGdc[biasOffset[i-1]+j] +=
                        layers[i+1].neurons[k].weights[j]
                      * (d2EdGdc[biasOffset[i]+k] * layers[i].neurons[j].dfdx
                      + dEdb[biasOnlyOffset[i]+k]
                      * layers[i].neurons[j].d2fdx2
                      * layers[i].neurons[j].dxdG);
                }
            }
            if (normalizeNeurons && i >= 1)
            {
                d2EdGdc[biasOffset[i-1]+j] /= layers[i].numNeuronsPrevLayer;
            }
        }
    }
 
    return;
}

References biasOffset, biasOnlyOffset, nnp::NeuralNetwork::Neuron::d2fdx2, nnp::NeuralNetwork::Neuron::dfdx, nnp::NeuralNetwork::Neuron::dxdG, layers, nnp::NeuralNetwork::Layer::neurons, normalizeNeurons, numLayers, nnp::NeuralNetwork::Layer::numNeurons, nnp::NeuralNetwork::Layer::numNeuronsPrevLayer, outputLayer, nnp::NeuralNetwork::Neuron::value, weightOffset, and nnp::NeuralNetwork::Neuron::weights.

Referenced by calculateDFdc().

Here is the caller graph for this function:

◆ allocateLayer()

void NeuralNetwork::allocateLayer	(	Layer &	layer,
		int	numNeuronsPrevLayer,
		int	numNeurons,
		ActivationFunction	activationFunction
	)

private

Allocate a single layer.

Parameters

[in,out]	layer	Neural network layer to allocate.
[in]	numNeuronsPrevLayer	Number of neurons in the previous layer.
[in]	numNeurons	Number of neurons in this layer.
[in]	activationFunction	Activation function to use for all neurons in this layer.

This function is internally called by the constructor to allocate all neurons layer by layer.

Definition at line 721 of file NeuralNetwork.cpp.

{
    layer.numNeurons          = numNeurons;
    layer.numNeuronsPrevLayer = numNeuronsPrevLayer;
    layer.activationFunction  = activationFunction;
 
    layer.neurons = new Neuron[layer.numNeurons];
    for (int i = 0; i < layer.numNeurons; i++)
    {
        layer.neurons[i].x      = 0.0;
        layer.neurons[i].value  = 0.0;
        layer.neurons[i].dfdx   = 0.0;
        layer.neurons[i].d2fdx2 = 0.0;
        layer.neurons[i].bias   = 0.0;
        layer.neurons[i].dxdG   = 0.0;
        layer.neurons[i].count  = 0;
        layer.neurons[i].min    =  numeric_limits<double>::max();
        layer.neurons[i].max    = -numeric_limits<double>::max();
        layer.neurons[i].sum    = 0.0;
        layer.neurons[i].sum2   = 0.0;
        if (layer.numNeuronsPrevLayer > 0)
        {
            layer.neurons[i].weights = new double[layer.numNeuronsPrevLayer];
            for (int j = 0; j < layer.numNeuronsPrevLayer; j++)
            {
                layer.neurons[i].weights[j] = 0.0;
            }
        }
        else
        {
            layer.neurons[i].weights = 0;
        }
    }
 
    return;
}

Referenced by NeuralNetwork().

Here is the caller graph for this function:

◆ propagateLayer()

void NeuralNetwork::propagateLayer	(	Layer &	layer,
		Layer &	layerPrev
	)

private

Propagate information from one layer to the next.

Parameters

[in,out]	layer	Neuron values in this layer will be calculated.
[in]	layerPrev	Neuron values in this layer will be used as input.

This function is internally looped by propagate().

Definition at line 761 of file NeuralNetwork.cpp.

{
    double dtmp = 0.0;
 
    for (int i = 0; i < layer.numNeurons; i++)
    {
        dtmp = 0.0;
        for (int j = 0; j < layer.numNeuronsPrevLayer; j++)
        {
            dtmp += layer.neurons[i].weights[j] * layerPrev.neurons[j].value;
        }
        dtmp += layer.neurons[i].bias;
        if (normalizeNeurons)
        {
            dtmp /= layer.numNeuronsPrevLayer;
        }
 
        layer.neurons[i].x = dtmp;
        if (layer.activationFunction == AF_IDENTITY)
        {
            layer.neurons[i].value  = dtmp;
            layer.neurons[i].dfdx   = 1.0;
            layer.neurons[i].d2fdx2 = 0.0;
        }
        else if (layer.activationFunction == AF_TANH)
        {
            dtmp = tanh(dtmp);
            layer.neurons[i].value  = dtmp;
            layer.neurons[i].dfdx   = 1.0 - dtmp * dtmp;
            layer.neurons[i].d2fdx2 = -2.0 * dtmp * (1.0 - dtmp * dtmp);
        }
        else if (layer.activationFunction == AF_LOGISTIC)
        {
            if (dtmp > EXP_LIMIT)
            {
                layer.neurons[i].value  = 1.0;
                layer.neurons[i].dfdx   = 0.0;
                layer.neurons[i].d2fdx2 = 0.0;
            }
            else if (dtmp < -EXP_LIMIT)
            {
                layer.neurons[i].value  = 0.0;
                layer.neurons[i].dfdx   = 0.0;
                layer.neurons[i].d2fdx2 = 0.0;
            }
            else
            {
                dtmp = 1.0 / (1.0 + exp(-dtmp));
                layer.neurons[i].value  = dtmp;
                layer.neurons[i].dfdx   = dtmp * (1.0 - dtmp);
                layer.neurons[i].d2fdx2 = dtmp * (1.0 - dtmp)
                                        * (1.0 - 2.0 * dtmp);
            }
        }
        else if (layer.activationFunction == AF_SOFTPLUS)
        {
            if (dtmp > EXP_LIMIT)
            {
                layer.neurons[i].value  = dtmp;
                layer.neurons[i].dfdx   = 1.0;
                layer.neurons[i].d2fdx2 = 0.0;
            }
            else if (dtmp < -EXP_LIMIT)
            {
                layer.neurons[i].value  = 0.0;
                layer.neurons[i].dfdx   = 0.0;
                layer.neurons[i].d2fdx2 = 0.0;
            }
            else
            {
                dtmp = exp(dtmp);
                layer.neurons[i].value  = log(1.0 + dtmp);
                dtmp = 1.0 / (1.0 + 1.0 / dtmp);
                layer.neurons[i].dfdx   = dtmp;
                layer.neurons[i].d2fdx2 = dtmp * (1.0 - dtmp);
            }
        }
        else if (layer.activationFunction == AF_RELU)
        {
            if (dtmp > 0.0)
            {
                layer.neurons[i].value  = dtmp;
                layer.neurons[i].dfdx   = 1.0;
                layer.neurons[i].d2fdx2 = 0.0;
            }
            else
            {
                layer.neurons[i].value  = 0.0;
                layer.neurons[i].dfdx   = 0.0;
                layer.neurons[i].d2fdx2 = 0.0;
            }
        }
        else if (layer.activationFunction == AF_GAUSSIAN)
        {
            double const tmpexp = exp(-0.5 * dtmp * dtmp);
            layer.neurons[i].value  = tmpexp;
            layer.neurons[i].dfdx   = -dtmp * tmpexp;
            layer.neurons[i].d2fdx2 = (dtmp * dtmp - 1.0) * tmpexp;
        }
        else if (layer.activationFunction == AF_COS)
        {
            double const tmpcos = cos(dtmp);
            layer.neurons[i].value  = tmpcos;
            layer.neurons[i].dfdx   = -sin(dtmp);
            layer.neurons[i].d2fdx2 = -tmpcos;
        }
        else if (layer.activationFunction == AF_REVLOGISTIC)
        {
            dtmp = 1.0 / (1.0 + exp(-dtmp));
            layer.neurons[i].value  = 1.0 - dtmp;
            layer.neurons[i].dfdx   = dtmp * (dtmp - 1.0);
            layer.neurons[i].d2fdx2 = dtmp * (dtmp - 1.0) * (1.0 - 2.0 * dtmp);
        }
        else if (layer.activationFunction == AF_EXP)
        {
            dtmp = exp(-dtmp);
            layer.neurons[i].value  = dtmp;
            layer.neurons[i].dfdx   = -dtmp;
            layer.neurons[i].d2fdx2 = dtmp;
        }
        else if (layer.activationFunction == AF_HARMONIC)
        {
            layer.neurons[i].value  = dtmp * dtmp;
            layer.neurons[i].dfdx   = 2.0 * dtmp;
            layer.neurons[i].d2fdx2 = 2.0;
        }
        layer.neurons[i].count++;
        dtmp = layer.neurons[i].x;
        layer.neurons[i].min  = min(dtmp, layer.neurons[i].min);
        layer.neurons[i].max  = max(dtmp, layer.neurons[i].max);
        layer.neurons[i].sum  += dtmp;
        layer.neurons[i].sum2 += dtmp * dtmp;
    }
 
    return;
}

Referenced by propagate().

Here is the caller graph for this function:

Member Data Documentation

◆ normalizeNeurons

bool nnp::NeuralNetwork::normalizeNeurons

private

If neurons are normalized.

Definition at line 407 of file NeuralNetwork.h.

Referenced by calculateD2EdGdc(), calculateDEdb(), calculateDEdc(), calculateDEdG(), calculateDxdG(), NeuralNetwork(), propagateLayer(), and setNormalizeNeurons().

◆ numWeights

int nnp::NeuralNetwork::numWeights

private

Number of NN weights only.

Definition at line 409 of file NeuralNetwork.h.

Referenced by getMemoryUsage(), getNumWeights(), info(), and NeuralNetwork().

◆ numBiases

int nnp::NeuralNetwork::numBiases

private

Number of NN biases only.

Definition at line 411 of file NeuralNetwork.h.

Referenced by calculateDFdc(), getNumBiases(), info(), and NeuralNetwork().

◆ numConnections

int nnp::NeuralNetwork::numConnections

private

Number of NN connections (weights + biases).

Definition at line 413 of file NeuralNetwork.h.

Referenced by calculateDEdc(), calculateDFdc(), getNumConnections(), info(), initializeConnectionsRandomUniform(), and NeuralNetwork().

◆ numLayers

int nnp::NeuralNetwork::numLayers

private

Total number of layers (includes input and output layers).

Definition at line 415 of file NeuralNetwork.h.

Referenced by calculateD2EdGdc(), calculateDEdb(), calculateDEdc(), calculateDxdG(), getConnections(), getMemoryUsage(), getNeuronStatistics(), getNumNeurons(), info(), modifyConnections(), NeuralNetwork(), propagate(), resetNeuronStatistics(), setConnections(), writeConnections(), and ~NeuralNetwork().

◆ numHiddenLayers

int nnp::NeuralNetwork::numHiddenLayers

private

Number of hidden layers.

Definition at line 417 of file NeuralNetwork.h.

Referenced by calculateDEdG(), and NeuralNetwork().

◆ weightOffset

int* nnp::NeuralNetwork::weightOffset

private

Offset adress of weights per layer in combined weights+bias array.

Definition at line 419 of file NeuralNetwork.h.

Referenced by calculateD2EdGdc(), calculateDEdc(), NeuralNetwork(), and ~NeuralNetwork().

◆ biasOffset

int* nnp::NeuralNetwork::biasOffset

private

Offset adress of biases per layer in combined weights+bias array.

Definition at line 421 of file NeuralNetwork.h.

Referenced by calculateD2EdGdc(), calculateDEdc(), NeuralNetwork(), and ~NeuralNetwork().

◆ biasOnlyOffset

int* nnp::NeuralNetwork::biasOnlyOffset

private

Offset adress of biases per layer in bias only array.

Definition at line 423 of file NeuralNetwork.h.

Referenced by calculateD2EdGdc(), calculateDEdb(), NeuralNetwork(), and ~NeuralNetwork().

◆ inputLayer

Layer* nnp::NeuralNetwork::inputLayer

private

Pointer to input layer.

Definition at line 425 of file NeuralNetwork.h.

Referenced by NeuralNetwork(), and setInput().

◆ outputLayer

Layer* nnp::NeuralNetwork::outputLayer

private

Pointer to output layer.

Definition at line 427 of file NeuralNetwork.h.

Referenced by calculateD2EdGdc(), calculateDEdb(), calculateDEdc(), getOutput(), modifyConnections(), and NeuralNetwork().

◆ layers

Layer* nnp::NeuralNetwork::layers

private

Neural network layers.

Definition at line 429 of file NeuralNetwork.h.

Referenced by calculateD2EdGdc(), calculateDEdb(), calculateDEdc(), calculateDEdG(), calculateDFdc(), calculateDxdG(), getConnections(), getNeuronStatistics(), getNumNeurons(), info(), modifyConnections(), NeuralNetwork(), propagate(), resetNeuronStatistics(), setConnections(), writeConnections(), and ~NeuralNetwork().

The documentation for this class was generated from the following files:

/home/runner/work/n2p2/n2p2/src/libnnp/NeuralNetwork.h
/home/runner/work/n2p2/n2p2/src/libnnp/NeuralNetwork.cpp

Classes

Public Types

Public Member Functions

Private Member Functions

Private Attributes

Detailed Description

Member Enumeration Documentation

◆ ActivationFunction

◆ ModificationScheme

Constructor & Destructor Documentation

◆ NeuralNetwork()

◆ ~NeuralNetwork()

Member Function Documentation

◆ setNormalizeNeurons()

◆ getNumNeurons()

◆ getNumConnections()

◆ getNumWeights()

◆ getNumBiases()

◆ setConnections()

◆ getConnections()

◆ initializeConnectionsRandomUniform()

◆ modifyConnections() [1/2]

◆ modifyConnections() [2/2]

◆ setInput() [1/2]

◆ setInput() [2/2]

◆ getOutput()

◆ propagate()

◆ calculateDEdG()

◆ calculateDEdc()

◆ calculateDFdc()

◆ writeConnections()

◆ getNeuronStatistics()

◆ resetNeuronStatistics()

◆ getMemoryUsage()

◆ info()

◆ calculateDEdb()

◆ calculateDxdG()

◆ calculateD2EdGdc()

◆ allocateLayer()

◆ propagateLayer()

Member Data Documentation

◆ normalizeNeurons

◆ numWeights

◆ numBiases

◆ numConnections

◆ numLayers

◆ numHiddenLayers

◆ weightOffset

◆ biasOffset

◆ biasOnlyOffset

◆ inputLayer

◆ outputLayer

◆ layers